Data Structure and Algorithm

This page cover advanced topic. Ordered by roadmap and the best solution in later part.

Array and Strings#

# Using Hash
def twoSum(self, nums, target):
    seen = {}
    for i, v in enumerate(nums):
        remaining = target - v
        if remaining in seen:
            return [seen[remaining], i]
        seen[v] = i
    return []

# Using Set and Sliding Window
def lengthOfLongestSubstring(self, s: str) -> int:
    n = len(s)
    maxLength = 0
    charSet = set()
    left = 0
    
    for right in range(n):
        if s[right] not in charSet:
            charSet.add(s[right])
            maxLength = max(maxLength, right - left + 1)
        else:
            while s[right] in charSet:
                charSet.remove(s[left])
                left += 1
            charSet.add(s[right])
    
    return maxLength

# Using Map (Faster)
def lengthOfLongestSubstring(self, s: str) -> int:
    n = len(s)
    maxLength = 0
    charMap = {}
    left = 0
    
    for right in range(n):
        if s[right] not in charMap or charMap[s[right]] < left:
            charMap[s[right]] = right
            maxLength = max(maxLength, right - left + 1)
        else:
            left = charMap[s[right]] + 1
            charMap[s[right]] = right
    
    return maxLength

Linked List#

A linked list is a data structure that the node points to next node in list. Stack is FIFO, Queue is FIFO.

# Two pointers have distance of n. When the second pointer reach the end, the first pointer is the nth node from the end.
def removeNthFromEnd(self, head, n):
    """
    :type head: Optional[ListNode]
    :type n: int
    :rtype: Optional[ListNode]
    """
    
    count = n
    dum = ListNode()
    dum.next = head
    ptr1 = ptr2 = dum

    if not head or count == 0:
        return head

    while ptr2.next:
        if count < 1:
            ptr1 = ptr1.next
        ptr2 = ptr2.next
        count -= 1
    ptr1.next = ptr1.next.next
    return dum.next

Hash#

Sometimes called as hash, hash map, map, unordered map, dictionary. A hash function maps a key to a value. It it consistent and irreversible. Suitable for quick key to value query but not the opposite.

Collision happens when two different key maps to the same value. In open addressing, the collided keys are mapped to a new index. Linear probing maps to next free index. Double hashing maps the value again with a offset. Quadratic probing maps to next offset in quadratic sequence until a free index is found. In closed addresing, a linked list is used for collided keys.

Tree#

Binary Search Tree#

Binary tree index nodes in an array in BFS order.The left node of i is i*2 + 1 and right node of i: i*2 +2. Binary search tree is a binary tree where the value of the left node is less than the root node and the value of the right node is greater than the root node. This have complexity of O(log n) for search.

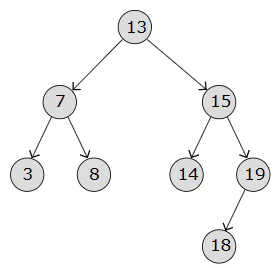
It’s straight forward to insert a node. To delete a node, there’s 3 condition.

1. If node is leaf, delete it.
2. If node has one child, replace the node with its child.
3. If node has two children, find the minimum value of the right subtree (in-order traversal first successor) and replace the node with it.

Answer Tree:
    3
   / \
  9  20
     / \
    15  7

Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]

The first node in preorder is 3, which is the starting node. All the nodes before 3 in inorder are the left subtree of inorder and preorder.

The third node in preorder is 20. All the nodes before 20 in inorder are the left subtree of inorder and preorder.

# A hash mapping stores the the number as key and index as value for inorder. Construct the binary tree by preorder traversal.
def buildTree(self, preorder, inorder):
        """
        :type preorder: List[int]
        :type inorder: List[int]
        :rtype: Optional[TreeNode]
        """
        
        p = deque(preorder)
        h = {}
        for i in range(len(inorder)):
            h[inorder[i]] = i

        def build(s, e):
            if s > e:
                return None
            m = h[val]
            root = TreeNode(p.popleft())
            root.left = build(s, m - 1)
            root.right = build(m + 1, e)
            return root
        
        return build(0, len(preorder)  - 1)

# The key is the current index of node in postorder must be greater than the index of parent node in preorder. Traverse the binary tree by postorder traversal.
def constructFromPrePost(self, preorder, postorder):
    """
    :type preorder: List[int]
    :type postorder: List[int]
    :rtype: Optional[TreeNode]
    """
    po = list(postorder)
    pr = {}
    for i, n in enumerate(preorder):
        pr[n] = i
    
    def build(i):
        parent_index = pr[i]
        if not po:
            return None
        else:
            current_node = po[-1]
        if pr[current_node] < parent_index:
            return None

        root = TreeNode(po.pop())
        root.right = build(current_node) 
        root.left = build(current_node) 

        return root
    
    return build(po[-1])

Radix Tree#

Stores prefix in an efficient way.

    api/
  /      \
user/  product/
/  \    /   \
id get  id get

Heap (Priority Queue)#

A min(max) heap is a tree that the children of a node is always greater(lesser) than or equal to its parent. The root is the minimum(maximum) value. This have complexity of O(log n) for insert and delete.

Initially, a binary tree looks like this. Let’s make a max heap.

        10
    /    \
    20      5
/  \    / \
6    1  8   9

Heapify starts at the last non-leaf node and move upwards. In this case, start from 20. It’s childern is less than 20. Move upwards, 20 is greater than 10, so swap.

        20
    /    \
    10      5
/  \    / \
6    1  8   9

Continue until a maxheap is created.

        20
    /    \
    10      5
/  \    / \
6    1  8   9

After inserting a node, heap to the root. After delete the root node, move the final leaf to the root and heap.

AVL Tree#

Derived from BST. But it keeps the balance of the tree when a node is inserted by making sure difference between left and right subtree is less than 2. Balance Factor, BF = height of left subtree - height of right subtree. If BF > 0, the node is right heavy. If BF < 0, the node is left heavy.

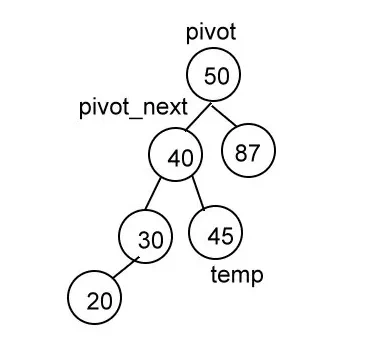
temp = pivot_next.rlink
pivot_next.rlink = pivot
pivot.llink = temp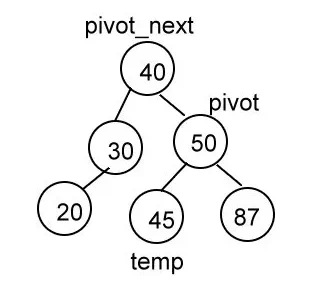

Red-black Tree#

Similar to AVL, but do lesser operation for insert and delete. AVL is better for frequent search with balanced tree.

Rules

1. New node is always red
2. Root is always black
3. All leaves including null are black
4. Nodes must be red or black
5. Child of red must be black
6. All path from root to leaves must has the same number of black nodes

Operations for Fixing Violation

1. If parent and uncle are red, make parent and uncle black and grandparent red. Then, fix at gradparent.
2. If uncle is black, node is grandparent right(left) of right(left) child, make parent black and grandparent red and rotate left(right) at gradparent. Then, fix at grandparent.
3. If uncle is black, node is grandparent left(right) of right(left) child, rotate left(right) at parent (This leads to 2). Then, fix at parent.

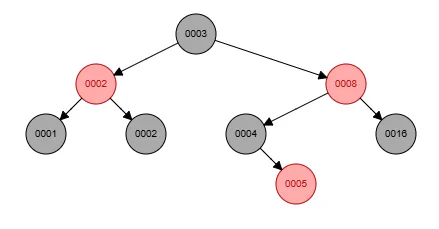
Imagine inserting on this sequence: 16, 8, 4, 2, 1, 3, 2, 5

Reference: Intro, Detail, visualization

Fenwick Tree#

Efficiently compute prefix sum. For search and insert, it takes O(log n).

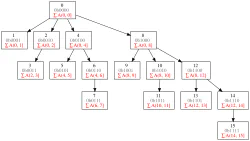
Properties

a = [1, 2, ... , n]

lsb(i) = i & -i (& denotes bitwise AND)

Parent of node i = i - lsb(i) = i & (i-1). Try to observe the bits in the image, what the lsb is doing.

At level k, there is C(log2 n, k) combination of nodes. Ex: C(3, 2) = 2^0 + 2^1, 2^0 + 2^2, 2^1 + 2^ = (3, 5, 6)

A node have lsb(i) 

F[i] = sum of `(a[i - lsb(i)], a[i]]`

# Interrogation (Query)

To search a range of prefix sum, let say i, j = [7, 8]. The common ancestor must be j - lsb(j), that is 0. Subtract F[j] from F[i]. Currently, F[8] contains sum of `a(0, 8]`, F[7] contains sum of 7. Then we continue iterate so new_i = i - lsb(i), which is the parent of F[i]. Now new_i is 6, we subtract (F[8] - F[7]) from F[6]. F[6] contains sum of 5 and 6. Continue until i != j - lsb(j). We will get the prefix sum of 8 and 7. That results in a[8]

# Update

Here, the parent of a node is different: i + lsb(i) = (i|(i - 1)) + 1. Let say we update node 6 by +3. The parent of 6 is 8. Change F[6] += 3. Then, continue update i's parent recursively until i exceed n. The parent of 6 is 8. Change F[8] += 3. The parent of 8 is 16. We stop here.

When we search F[1, 5] theres no update. When we search F[6], we include the updated value. When we search F[7], it will adds the parents: F[4], F[6], F[7], the updated value is included. When we search F[14], it will adds the parents: F[8], F[12], F[14], the updated value is included.

# Search Rank

Given a prefix sum, we can calculate rank in O(log n). Nodes with odd indexes lsb⁡(i) = 1 are leaves. Node i parent is (i - lsb(i) | 2 lsb(i)), node i child is i +- lsb(i) / 2. It looks like this:

      4
    /    \
  2      6
/  \    / \
1   3  5   7

Let say we want to find rank of an integer F[3]. Start at root, F[3] < F[4], traverse left. F[3] > F[2], traverse right. Now we got the answer. The index of 3 is 6. From index 6, we can calculate the rank is 3.

Graph#

Shortest Path#

Dijkstra’s Algorithm

Find shortest path from one vertex to all other vertex. Does not work for negative edge weight.

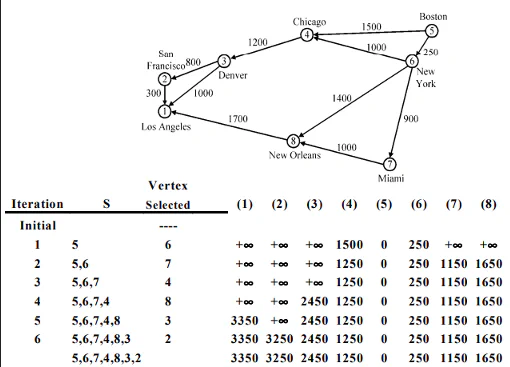
Find min{current cost from v to u, cost from current vertex to u}

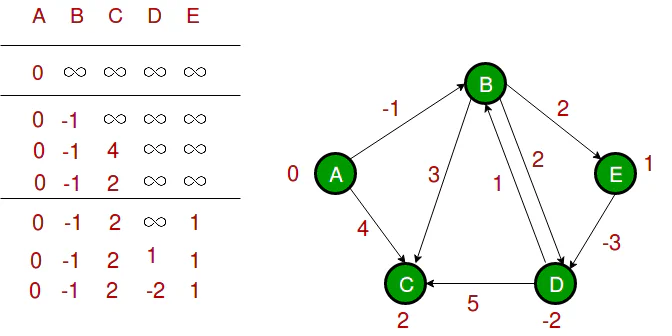
Bellman-Ford Algorithm

Find shortest path from one vertex to all other vertex. Work for negative edge weight. Slower than Dijkstra. If dist[v] > dist[u] + weight of edge uv, then update dist[v]

Floyd-Warshall Algorithm

Finds shortest path from every vertex to all other vertex. Work for negative edge weight. Slower than Dijkstra and Bellman-Ford. In a matrix i,j, if (i, k) + (k, j) < (i, j), then update.

A Search*

At a node, approximate the distance of the next node to the goal. Then pick the shortest approximate.

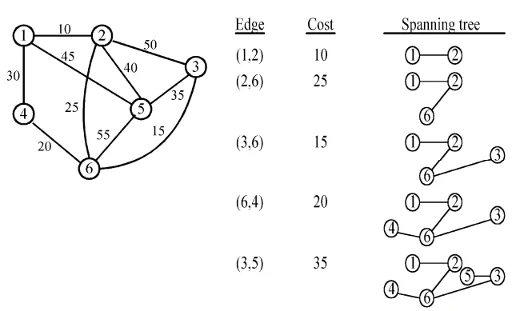
Minimum Spanning Tree#

A tree in a graph that only contains all of the vertex of the graph with smallest total weight

Kruskal’s algorithm

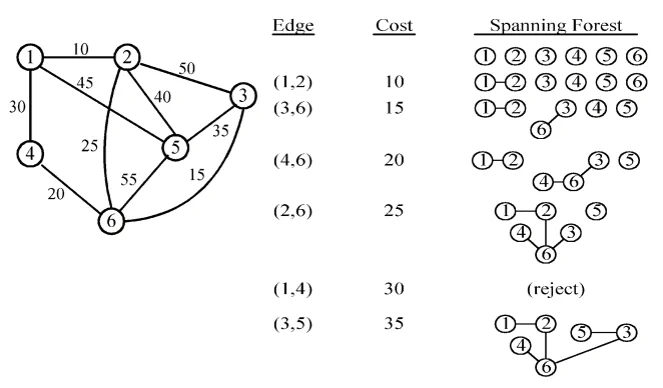
1. Select edge with smallest weight
2. Add the next smallest weight edge to forest if it does not cause a cycle
3. Stop if there is n-1 edges, else goto step 2

Prim’s Algorithm

1. x in V, A = {x}, B = V - {x}
2. Select (u, v) where u in X, v in Y such that (u, v) has smallest weight between A and B. Memorizing the minimal discovered edge
3. Put (u, v) in tree. A = A U {v}, B = B - {v}
4. If B = empty, stop, else, go to step 2

Cycle Basic#

Cycle basis is set of cycles that can generate every cycle in graph using ring sum operator (linear combination).

1. Determine size of minimal cycle basis as k
2. Find all cycles and sort by weight. Add cycles to cycle basis one by one if it cannot be formed by combination of some cycles already in cycle basis. Using Gaussian Elimination
3. Stop if cycle basis has k cycles

k= |Edge Count| − (|Vertex Count| − 1)

Sort#

def quicksort(arr):
    if len(arr) <= 1:
        return arr
    else:
        pivot = arr[0]
        # all element lesser than pivot is put into this array
        less = [x for x in arr[1:] if x <= pivot] 
        # all element greater than pivot is put into this array
        greater = [x for x in arr[1:] if x > pivot]
        return quicksort(less) + [pivot] + quicksort(greater)
unsorted_array = [3, 6, 8, 10, 1, 2, 1]
sorted_array = quicksort(unsorted_array)
print("Unsorted array:", unsorted_array)
print("Sorted array:", sorted_array)

Recursive#

Divide and Conquer#

Divide problem into subproblem resursively.

2D-Rank Finding O(n log n)

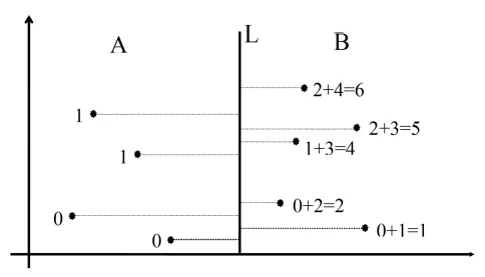
1. Sort all points based on x then y
2. Find median line
3. Find ranks of points in A and B recursively
4. Update ranks of points B when the y value of points in B is greater than A

Closest Pair Problem O(n log n)

Find the closest point in a graph of points. Source.

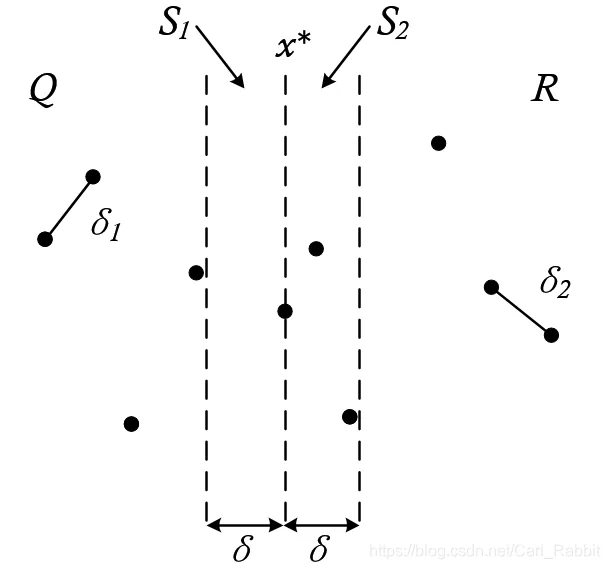
1. Pick a median x point and divide into 2 part recursively. Use brutal when points <= 3
2. On merging, find the min pairs from SL(left region), SR(right region), or closest pair that lies in (median + d, median - d). d is the min pair distance in SL and SR. Let p be a point in SL, the y of q in SR side of slab must be in between [p.y + d, p.y - d]

Convex Hull - Graham’s Scan (Greedy)

Find smallest convex polygon containing all of the points.

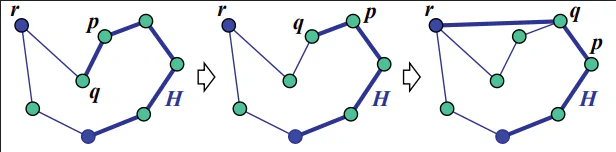
1. Find lowest point. O(n)
2. Form nonintersecting polygon by sorting the points counterclockwise. O(n log n)
3. Remove nonconvex vertex. O(n)

Voronoi Diagram

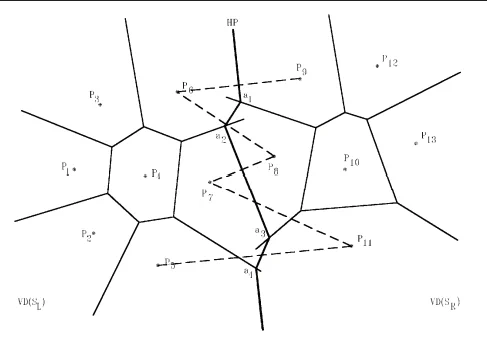
Branch and Bound#

Personnel Assignment Problem

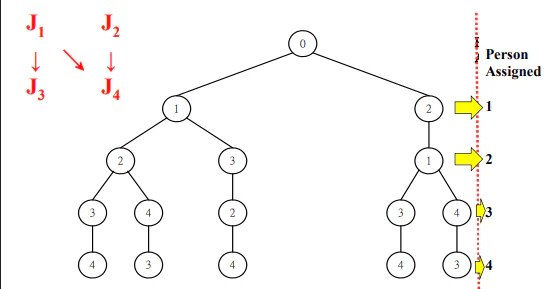
Each personal work each jobs at different cost. Some jobs need to be done before other jobs. Use topological sort to display as branch.

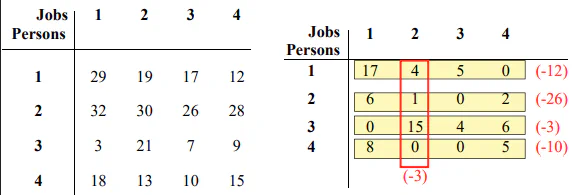
Calculate reduced cost matrix. So that in every branch and bound, we can determine which branch have minimum lower bound.

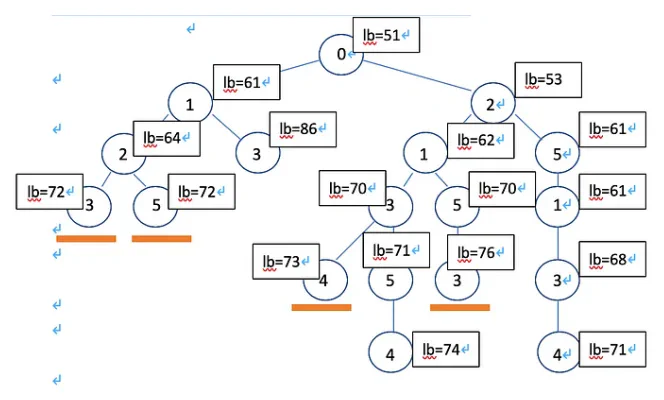
The final flow is 0, 2, 5, 1, 3, 4 because at each branch, the node have lower bound.

Learn further about this concept on travelling salesman problem.

Knapsack Problem (Branch and Bound)

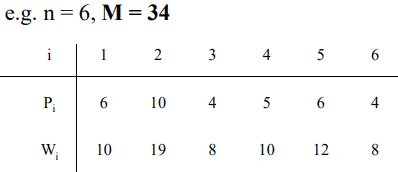
The upper bound found by a feasible solution. (Picks the most points first). The lower bound is found greedy. (Calculate the density and get allowing weights to be fractured, P1 + P2 + 5/8 P3).

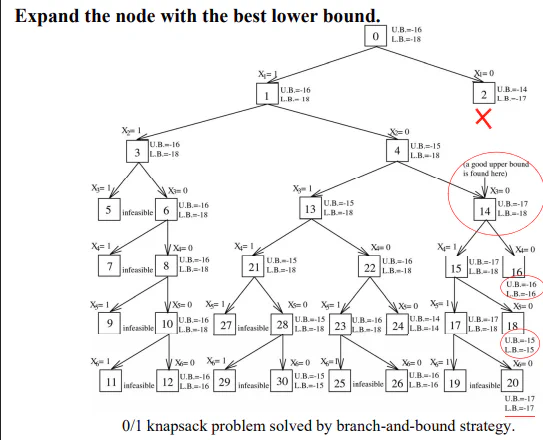
Linear Programming (Prune and Search)

Slice things.

Dynamic Programming#

Use memory to save computated values for future use.

Longest Common Subsequence

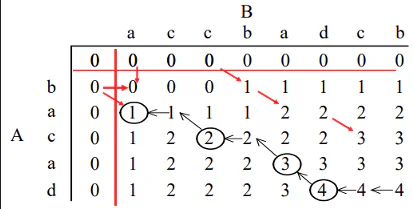
A = "bacad", eg: ad, ac, bac, acad, bacad, bcd
B = "accbadcb", eg: ad, ac, bac, acad
LCS of A and B: acad

Knapsack

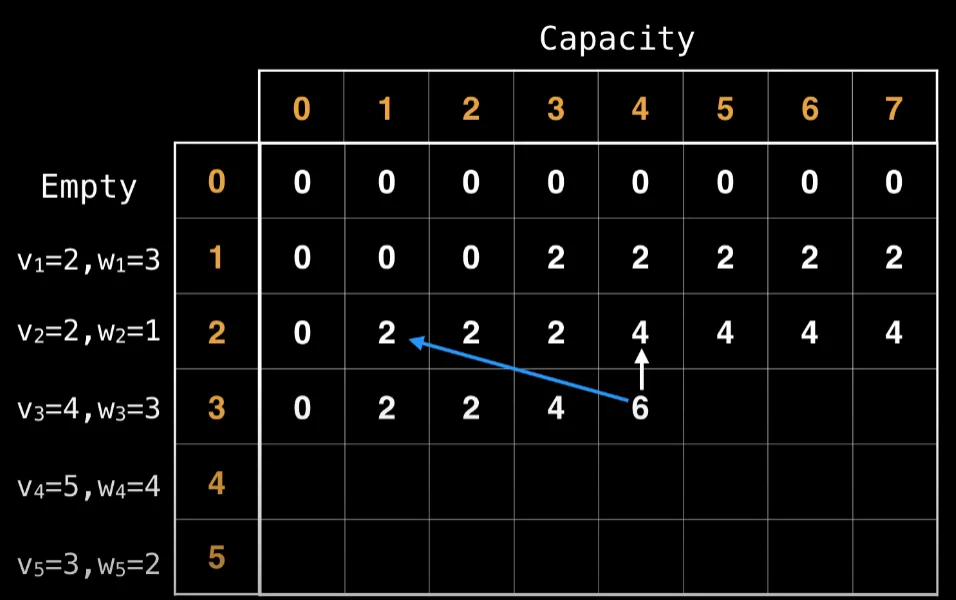
i is the total weight, j is the turn of items. In each turn, the vertical arrow suggest now taking that item, the diagonal shift suggest taking that item by shifting n units to the left by the weight. The cell indicates the maximum value of not taking the item (vertical) or take the item max value at reduced weight + current value (diagonal).

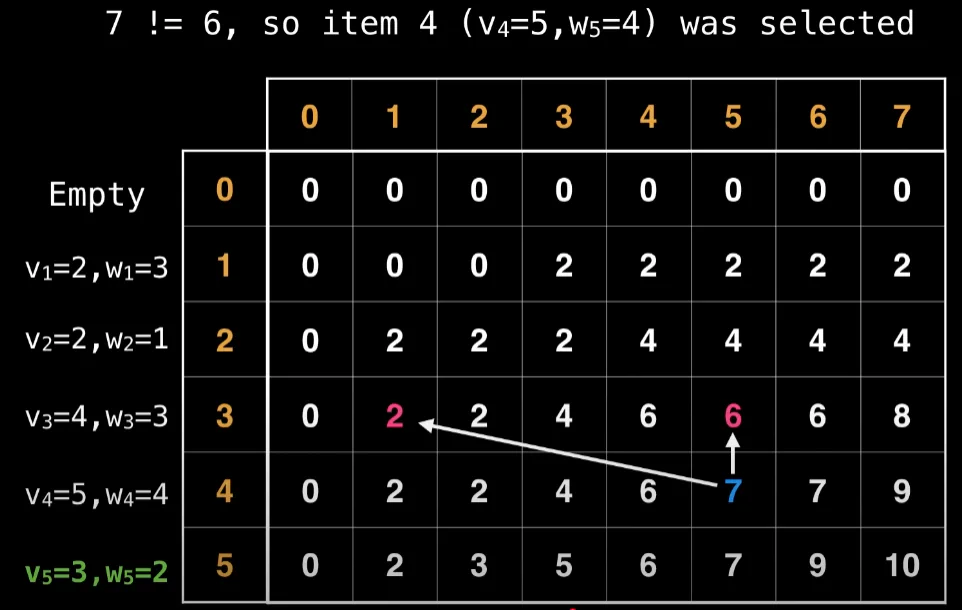
To find the optimal results, if the vertical arrow shows same number as the cell. Don’t take that item.

def maxProduct(self, nums):
    """
    :type nums: List[int]
    :rtype: int
    """
    res = max(nums)
    cur_max = cur_min = 1
    for n in nums:
        ma = cur_max * n
        mi = cur_min * n
        cur_max = max(ma, mi, n)
        cur_min = min(ma, mi, n)
        res = max(res, cur_max)

    return res

# Replacing an element (Let's sat 3 replace 5, because both are greater than 2) in the result lis did not increae the number of LIS.
def lengthOfLIS(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        def binarySearch(key, li):
            left = 0
            right = len(li) - 1
            while left <= right:
                m = (left + right) // 2
                if key > li[m]:
                    left = m + 1
                elif key < li[m]:
                    right = m - 1
                else:
                    return m
            return left
        
        lis = list()

        for i in range(len(nums)):
            n = nums[i]
            if not lis or lis[-1] < n:
                lis.append(n)
            else:
                inx = binarySearch(n, lis)
                lis[inx] = n

        return len(lis)

Backtracking#

Backtracking is a problem-solving algorithmic technique that involves finding a solution incrementally by trying different options and undoing them if they lead to a dead end.

Advanced Data Structure#

Randomized Algorithm#

Use randomess to solve problems.

Rabin-Karp Algorithm#

A string-searching algorithm that uses hashing.

text = ABCDEFCDE
pattern = CDE
result = [2, 6] (index of substring is same as pattern)

# Steps

Let a = 1, b = 2, ...
Hash(CDE) = (a * 100 + b * 10 + c) mod 13 = 7 = Hash(pattern) 
Hash(ABC) = (1 * 100 + 2 * 10 + 3) mod 13 = 6
Hash(BCD) = (2 * 100 + 3 * 10 + 4) mod 13 = 0   # This can be optimized to improve from O(mn) to O(m + n) as below
Hash(BCD) = ( (Hash(BDC) - a * 100) * 10 + d ) mod 13 = 0
Hash(BCD) = ( (0 - 1 * 100) * 10 + 4 ) mod 13 = 0

If Hash(pattern) = Hash(CDE), check manually if the substring is same.

Knuth-Morris-Pratt Algorithm#

This algorithm is efficient for finding number of occurence of a pattern in a string in O(n). It creates an auxiliary array (LPS) for the pattern that store the previous starting point. Then, we iterate through the string and check if the pattern matches.

def lps(pattern):
    m = len(pattern)
    lps = [0] * m
    i, j = 1, 0
    while i < m:
        if pattern[i] == pattern[j]:
            j += 1
            lps[i] = j + 1
            i += 1
        else:
            if j == 0:
                lps[i] = 0
                i += 1
            else:
                j = lps[j - 1]
    return lps

def kmp(text, pattern):
    n = len(text)
    m = len(pattern)
    lps = lps(pattern)
    i = j = 0
    while i < n:
        if text[i] == pattern[j]:
            i += 1
            j += 1
        if j == m:
            print("Found at: ", i - j)
            j = lps[j - 1]
        else:
            if i < n and text[i] != pattern[j]:
                if j == 0:
                    i += 1
                else:
                    j = lps[j - 1]
            else:
                i += 1    

Segment Tree#

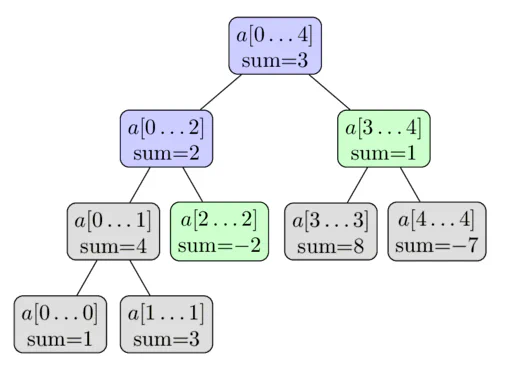
Stores range values. The picture shows finding sum of interval [2, 4] by adding a[2…2] and a[3…4]. To update a value, iterate the update using divide and conquer.

Disjoint Set Union (DSU) / Union-Find: Excellent for problems involving connectivity or partitioning into sets.

Segment Tree: A powerful tool for handling range queries and updates on an array.

Topological Sorting（拓撲排序）：任務排程、編譯順序、依賴解決

Max Flow / Min Cut（Ford-Fulkerson, Edmonds-Karp, Dinic）：資源分配、網路流、圖像分割

Strongly Connected Components（Tarjan / Kosaraju）：程序分析、模組依賴分析

Union-Find（Disjoint Set Union）：連通元件、群組管理

Graph Coloring / Bipartite Checking：資源衝突避免、分組問題

Longest Increasing Subsequence / Substring problems

Tree DP：用在圖論 + 樹結構問題

Bitmask DP：狀態壓縮，解 NP-hard approximation（如旅行推銷員問題 TSP）

Digit DP / Interval DP / Memory-efficient DP：各種複雜變形

⛓️ 三、數學與組合優化（尤其在 AI/ML、理論、密碼學會遇到） 線性規劃（Linear Programming / Simplex）

貪婪演算法正當性分析（Greedy correctness with Matroids）

組合數學與生成函數（Combinatorics, Generating Functions）

模數運算、快速冪、GCD 擴展應用（數論技巧）

Trie + Bit Trie：字串查詢、異或最大化

Suffix Array / Suffix Tree / LCP：字串處理、基因比對、壓縮

Persistent Data Structures（不可變結構）: 時間旅行、版本控制

Gradient Descent（GD, SGD, Adam）與收斂條件

Convex Optimization / Lagrange Multiplier

Expectation Maximization（EM）

K-means、DBSCAN、Spectral Clustering

Online Algorithms / Competitive Analysis：做即時決策

Parallel / Distributed Algorithms：多執行緒、GPU 編程、MapReduce